一.算术平方根：

1.定义：一般地说，若一个非负数x的平方等于a，即x2=a，则这个数x叫做a的

算术平方根

。

规定：0的算术平方根为0

例：3^2=9, 3就叫做9的算术平方根

2.表示：一个非负数a的算术平方根可表示为

“√a”

，读作

"根号a"

，a叫做被开方数

3.性质：

正数的算术平方根是正数

0的算术平方根是0

负数没有算术平方根

双重非负性

：

√a≥0且a≥0

4.算术平方根等于它本身的数有：

0和1

二.平方根：

1.定义：若一个数x的平方等于a，则这个数叫做a的

平方根

。

若x2=a，则x叫做a的平方根

2.表示：一个非负数a的平方根可以表示为“

±√a

”

3.性质：

正数有两个平方根，他们互为相反数

0的平方根是0

负数没有平方根

4.开平方：求一个数a的平方根的运算，叫做开平方，开平方是平方的逆运算

平方根等于它本身的数：0

区别：9的平方根为±3 ；9的算术平方根为3，正数的平方根都是前面加±，算术平方根全部都是非负数

三. 立方根

1.定义

： 如果一个数的立方等于a，那么这个数叫a的

立方根

，也称为三次方根，也就是说，如果x3=a,那么x叫做a的立方根。

【注意】在平方根中的根指数2可省略不写，但立方根中的根指数3不能省略不写。

2.表示

：?a读作"三次根号a"其中，a叫做被开方数，3叫做根指数。

3.性质

：

• 正数的立方根是正数
• 0的立方根是0
• 负数的立方根是负数

4.开立方

：是求一个数的立方根的运算

5

.立方根等于本身的数为：

0和±1

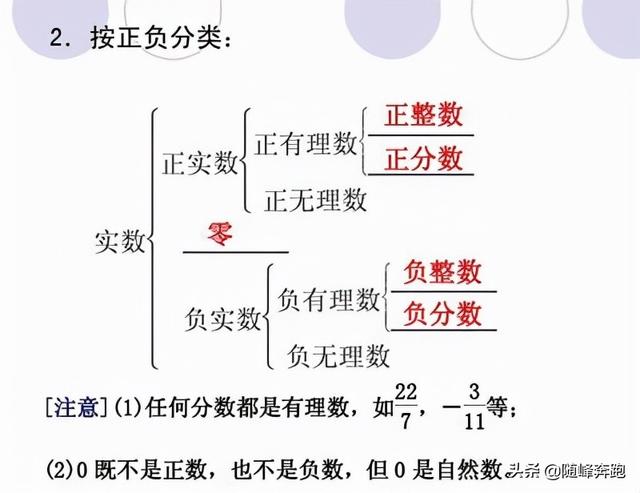
四.实数

1.无理数：无限不循环小数

例：√2，√3，π

2.实数，是有理数和无理数的总称

3.实数与数轴关系：

数轴上的点与实数成什么关系,即每一个实数都可以用数轴上的一个点来表示;

反过来,数轴上的每一个点都表示一个实数。

4.分类：